|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lins S. — Gems, computers, and attractors for 3-manifolds |
|
|
 |
| Предметный указатель |
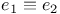 100 100
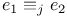 100 100
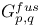 100 100
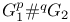 102 102
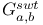 11 11
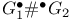 102 102
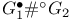 102 102
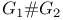 104 104
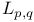 31 31
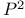 104 104
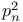 104 104
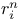 6 6
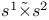 117 117
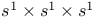 30 30
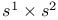 117 117
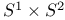 -normalization 263 -normalization 263
 104 104
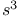 128 128
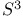 -normalization 263 -normalization 263
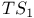 -move 11 -move 11
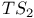 -move 11 -move 11
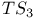 -move 11 -move 11
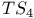 -move 12 -move 12
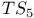 -move 12 -move 12
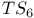 -move 13 -move 13
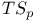 -class 189 -class 189
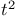 104 104
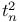 104 104
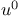 -forest of rigid 3-gems 182 -forest of rigid 3-gems 182
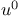 -move 14 154 -move 14 154
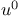 -representative of a 3-gem 142 -representative of a 3-gem 142
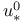 -move 14 154 -move 14 154
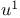 -move 14 154 -move 14 154
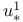 -move 14 154 -move 14 154
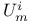 -move on G 145 -move on G 145
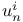 -attractor, an 89 -attractor, an 89
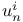 -attractor, the 89 -attractor, the 89
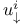 -move 145 -move 145
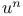 -class 15 -class 15
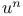 -classification 15 -classification 15
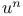 -essential, 3-gem 15 -essential, 3-gem 15
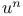 -move 14 154 -move 14 154
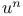 -reducible, 3-gem 15 -reducible, 3-gem 15
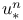 -move 14 154 -move 14 154
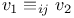 100 100
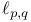 31 31
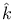 -residue 26 -residue 26
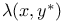 243 244 243 244
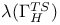 141 141
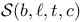 33 33
 -move 11 127 -move 11 127
 -pair 10 40 -pair 10 40
 -gem 5 53 -gem 5 53
 -symmetries 54 -symmetries 54
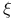 , the sum of the connectivities of surfaces 65 , the sum of the connectivities of surfaces 65
(n + 1)-graph 1
1-dipole 3 35
1-dipole creation 98
1-dipole in 2-gem 98
1-dipole moves 99
2-dipole 3 37
2-gem 19
3-crystallization 35
3-gem 2 20
A-move, 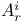 -move 131 -move 131
Admisible triple 261
Alternating presentation of a group 74
Attractor for a 2-manifold 104
Attractor for a 3-manifold 4
B-move, 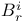 -move 131 -move 131
Baloon 39
Baloon move 39
Betti number of a 3-manifold 250
Bigon 2 16
Bipartiteness character of a graph 105
Blackboard framed link 81
Blink 8 81
Blink getting absorbed 85
Bond space of a digraph 106
Breaking of a duet 175
Breaking of a handle 122
Breaking of a trio 107
C-move, 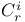 -move 132 -move 132
Cancellation of 1-dipole 35 98
Cancellation of 2-dipole 38
Canonical presentation of a 3-gem 63
Code of a 3-gem 30
Code of bipartite connected (n + 1)-graph 63
Code of bipartite non-connected (n + 1)-graph 64
Code of non-bipartite 3-gem 64
Code-colored edges of a 3-gem 127
Code-numbered vertices of a 3-gem 127
Color specification of a 3-page 130
Color specification of a ladder 130
Color specification of a quasi-cluster 130
Color specification of a quasi-cube 129
Color specification of a TS-configuration 129
Colored triangulation 38
Complementary handlebody 9
Complexity of a 3-gem 178
Complexity of a closed 3-manifold 178
Connected sum along p, q 102 114
Connectivity of a closed surface 65
| Contribution of a vertex 137
Creation of 1-dipole 35 98
Creation of 2-dipole 38
Crystallization 35
Cycle space of a digraph 106
D-move, 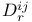 -move 132 -move 132
Depth-first search (DFS) exploration of a graph 60
Derived 3-gem 235 236
Digraph 106
Dual construction 3
Dual edge 106
Duet in (n + 1)-graph 175
E-move, 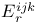 -move 133 -move 133
Equivalent 2-gems 99
Equivalent string presentations 55
Essential 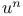 -class 15 -class 15
Euler characteristic 105
Expanded gist 54
F-move, 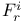 -move 133 -move 133
Face 21
Face of a graph embedded in a surface 17
Framed link 5 77
Free reduction 73
Fusible edge 172
Fusion at two vertices 100
Genus of a Heegaard splitting 66
Geometric dual 106
Handle 120
Handle free, 3-manifold 177
Handle slide 270
Handleboly 66
Heegaard diagram 66
Heegaard splitting 66
Horizontal move 15
ij-gon 16
Incidence matrix of a digraph 106
Intersection numbers 243
Involution 32
Involved colors in a dipole 38
Involved colors in dipoles 3
Irreducible 3-manifold 125
Isotopy, ambient 269
Isotopy, regular 269
L(p,q) 31
Linking matrix 264
Loop in a graph 106
Medial of a plane graph 256
monopole 13 142
Move 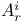 131 131
Move 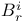 131 131
Move 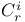 132 132
Move 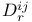 132 132
Move 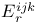 133 133
Move 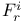 133 133
Mutability of a 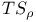 -class 189 -class 189
n-residue 2
Of a cellular embedding 21
Orientable prime manifold 103
Perfect group 4
Pillow 39
Pillow move 39
Planar 3-manifold 255
Preserving the orientation 53
Prime 3-manifold 113
q-deformed quantum factorial 261
q-deformed quantum integer 260
Quantum invariants 224
Quartet 120
Quaternionic space 34
r-admissible state 262
Reduced adjacency matrix of a 3-gem 42
Reducible 3-manifold 125
Ribbon move 270
Rigid  -gems 172 -gems 172
Rigid 3-gem 6 11 127
Root vertex of a 3-page 130
Root vertex of a ladder 130
Root vertex of a quasi-cluster 130
Root vertex of a quasi-cube 129
Root vertex of a TS-configuration 129
Size of a 3-gem 29
State 262
String presentation 5 52
String presentation equivalent to a 3-gem 55
String presentation for 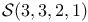 55 55
String presentation for a 3-gem 30
Strong component of a directed graph 155
Superattractor for a 3-manifold 4
Surface induced by 2-gem 97
Switching of a  -pair 40 -pair 40
Switching of a rho-pair 10
Symmetric space 118
System of meridian disks in a handlebody 68
Tidy matrix for a (3 + 1)-graph 147
Triball 20
Trio in (n + 1)-graph 107
TS-configuration, 3-page 13
TS-configuration, ladder 12
TS-configuration, quasi-cluster 12
TS-configuration, quasi-cube 11
TS-configurations 129
TS-moves 11
U-move 13
Walking triplet 100
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



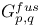
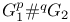
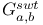
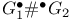
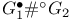
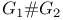
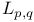
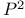
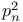
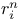
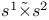
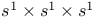
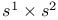
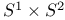 -normalization
-normalization 
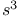
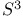 -normalization
-normalization 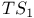 -move
-move 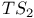 -move
-move 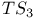 -move
-move 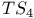 -move
-move 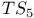 -move
-move 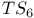 -move
-move 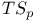 -class
-class 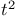
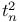
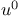 -forest of rigid 3-gems
-forest of rigid 3-gems 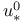 -move
-move 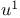 -move
-move 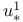 -move
-move 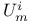 -move on G
-move on G 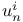 -attractor, an
-attractor, an 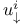 -move
-move 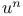 -class
-class 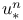 -move
-move 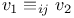
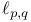
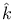 -residue
-residue 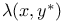
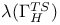
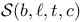
 -move
-move  -gem
-gem 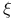 , the sum of the connectivities of surfaces
, the sum of the connectivities of surfaces 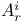 -move
-move 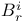 -move
-move 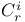 -move
-move 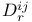 -move
-move 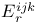 -move
-move 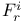 -move
-move 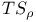 -class
-class