We investigate the uses of membranes in theoretical physics. Starting with the bosonic membrane and the formulation of its dynamics we then move forward in time to the introduction of supersymmetry. Matrix theory is introduced and a full proof of the continuous spectrum of the supermembrane is given. After this we deal with various concepts in M-theory (BPS-states, Matrix Theory, torodial compactifications etc.) that are of special importance when motivating the algebraic approach to M-theoretic calculations. 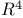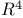This approach is then dealt with by first reviewing the prototypical example of the Type IIB amplitude and then the various issues of microscopic derivations of the corresponding results through first-principle computations in M-theory. This leads us to the mathematics of automorphic forms and the main result of this thesis, a calculation of the p-adic spherical vector in a minimal representation of