Авторизация
Поиск по указателям
Nesterov Y., Nemirovskii A. — Interior-Point Polynomial Algorithms in Convex Programming
Обсудите книгу на научном форуме Нашли опечатку?
Название: Interior-Point Polynomial Algorithms in Convex ProgrammingАвторы: Nesterov Y., Nemirovskii A. Аннотация: Written for specialists working in optimization, mathematical programming, or control theory. The general theory of path-following and potential reduction interior point polynomial time methods, interior point methods, interior point methods for linear and quadratic programming, polynomial time methods for nonlinear convex programming, efficient computation methods for control problems and variational inequalities, and acceleration of path-following methods are covered. In this book, the authors describe the first unified theory of polynomial-time interior-point methods. Their approach provides a simple and elegant framework in which all known polynomial-time interior-point methods can be explained and analyzed; this approach yields polynomial-time interior-point methods for a wide variety of problems beyond the traditional linear and quadratic programs.
The book contains new and important results in the general theory of convex programming, e.g., their "conic" problem formulation in which duality theory is completely symmetric. For each algorithm described, the authors carefully derive precise bounds on the computational effort required to solve a given family of problems to a given precision. In several cases they obtain better problem complexity estimates than were previously known. Several of the new algorithms described in this book, e.g., the projective method, have been implemented, tested on "real world" problems, and found to be extremely efficient in practice.
Special Features o the developed theory of polynomial methods covers all approaches known so far o presents detailed descriptions of algorithms for many important classes of nonlinear problems
Audience Specialists working in the areas of optimization, mathematical programming, or control theory will find this book invaluable for studying interior-point methods for linear and quadratic programming, polynomial-time methods for nonlinear convex programming, and efficient computational methods for control problems and variational inequalities. A background in linear algebra and mathematical programming is necessary to understand the book. The detailed proofs and lack of "numerical examples" might suggest that the book is of limited value to the reader interested in the practical aspects of convex optimization, but nothing could be further from the truth. An entire chapter is devoted to potential reduction methods precisely because of their great efficiency in practice.
Contents Chapter 1: Self-Concordant Functions and Newton Method; Chapter 2: Path-Following Interior-Point Methods; Chapter 3: Potential Reduction Interior-Point Methods; Chapter 4: How to Construct Self-Concordant Barriers; Chapter 5: Applications in Convex Optimization; Chapter 6: Variational Inequalities with Monotone Operators; Chapter 7: Acceleration for Linear and Linearly Constrained Quadratic Problems; Bibliography; Appendix 1; Appendix 2.
Язык: Рубрика: Computer science /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1994Количество страниц: 416Добавлена в каталог: 12.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Acceleration for linear and linearly constrained quadratic problems, main inequality 323 Acceleration for linear and linearly constrained quadratic problems, strategy 316 Acceleration for linear and linearly constrained quadratic problems, tactics 317 Advanced linear algebra 321 Barrier calculus 148 174 Barrier-generated family 2 Barrier-generated family, Legendre transformation 181 Barrier-generated family, superposition theorem 182 184 Boolean programming, dual bounds for 243 Combination rules for barriers/coverings, arithmetic summation 155 Combination rules for barriers/coverings, conic hull 149 Combination rules for barriers/coverings, direct products 149 Combination rules for barriers/coverings, images under affine mappings 152 Combination rules for barriers/coverings, intersections 149 Combination rules for barriers/coverings, inverse images under affine mappings 148 Combination rules for barriers/coverings, inverse images under nonlinear mappings 156 Combination rules for barriers/coverings, projective transformation 143 Combined volumetric barrier 203 246 Complementarity problem 277 381 Conic duality 103 Conic representation 175 Conic representation, second-order 224 Conic representation, second-order, examples 226 Constraint regularization scheme 218 Convex problem, conic form 102 147 188 Convex problem, conic form, complementary slackness relation 104 106 109 Convex problem, conic form, dual formulation 103 Convex problem, conic form, dual inequality 105 Convex problem, conic form, duality relations 105 Convex problem, conic form, duality theorem 109 Convex problem, conic form, normal primal-dual pair 106 Convex problem, conic form, primal-dual pair 104 Convex problem, conic form, primal-dual relations 107 Convex problem, conic form, zero duality gap 106 109 Convex problem, standard form 57 103 147 188 Convex-concave games 276 Coverings 175 Coverings, calculus 176 Coverings, calculus, direct product 178 Coverings, calculus, images 176 Coverings, calculus, intersections 178 Coverings, calculus, inverse images 176 Curvature condition 383 Differential inclusion 245 Dikin's ellipsoid 13 34 Dikin's method 379 Duality theorem 109 Eigenvalues minimization problems, largest of 239 242 Eigenvalues minimization problems, sum of k largest 239 Extremal ellipsoids, circumscribing minimal volume ellipsoid 270 Extremal ellipsoids, inscribing maximal volume ellipsoid 244 249 Extremal ellipsoids, inscribing maximal volume ellipsoid, algebraic formulation 250 Extremal ellipsoids, inscribing maximal volume ellipsoid, geometric formulation 249 Extremal ellipsoids, inscribing maximal volume ellipsoid, path-following method for finding 252 254 257 263 268 270 Function, 66 Function, fractional-quadratic 227 241 Function, Lyapunov's 101 Function, positive-semidefinite representable 237 Function, potential 101 112 124 139 Functional element 176 Functional element, Legendre transformation of 181 Linear differential equations, uniqueness theorem 14 Linear-fractional problems 121 Logarithmically homogeneous barriers, 40 Logarithmically homogeneous barriers, definition of 39 Logarithmically homogeneous barriers, Legendre transformation of 47 48 Logarithmically homogeneous barriers, main properties of 40 41 Lovasz capacity number of graph 242 Mappings, compatible with barrier 160 Mappings, compatible with convex domain 159 Mappings, compatible with convex domain, compatibility of superpositions 168 Mappings, compatible with convex domain, examples 160 165 Mappings, concave with respect to cone 156 Mappings, concave with respect to cone, examples 157 Mappings, maximal monotone 274 Mappings, monotone 273 Mappings, quadratic-fractional 166 Methods of centers 2 82 see "Potential Methods, barrier-generated 2 70 Methods, interior penalty function 1 379 Monotone element 274 Monotone element, potential 310 Monotone element, transformation rules for 311—313 Monotone operator, compatible with self-concordant barrier, definition of 291 Monotone operator, compatible with self-concordant barrier, properties of 291 292 Monotone operator, convex representation of 307 Monotone operator, linear monotone 304 Multistep barrier methods, acceleration based on optimal method for smooth convex optimization, efficiency estimate 336 Multistep barrier methods, acceleration based on optimal method for smooth convex optimization, scheme 334 Multistep barrier methods, conjugate-gradient-based acceleration, efficiency estimate 351 Multistep barrier methods, conjugate-gradient-based acceleration, scheme 348 Multistep barrier methods, fixed-point-based acceleration, efficiency estimate 342 Multistep barrier methods, fixed-point-based acceleration, scheme 340 Multistep barrier methods, gradient-descent-based acceleration, efficiency estimate 330 Multistep barrier methods, gradient-descent-based acceleration, scheme 329 Multistep barrier methods, sets 327 Nash equilibrium 276 Newton decrement, definition of 15 284 Newton decrement, properties of 16 Newton iterate 16 284 Newton method, convergence results 17 18 24 Newton method, damped 15 Newton method, stepsize rules 24 26 Path-following interior-point methods 57 Path-following interior-point methods, barrier-generated 65 68 Path-following interior-point methods, barrier-generated, efficiency estimate 75 Path-following interior-point methods, barrier-generated, large-step strategy 76 Path-following interior-point methods, barrier-generated, main stage 73 Path-following interior-point methods, barrier-generated, preliminary stage 70 Path-following interior-point methods, dual parallel trajectories method 86 87 Path-following interior-point methods, dual parallel trajectories method, efficiency estimate 92 Path-following interior-point methods, dual parallel trajectories method, scheme 90 91 Path-following interior-point methods, method of centers 80 Path-following interior-point methods, method of centers, efficiency estimate 84 Path-following interior-point methods, method of centers, scheme 84 Path-following interior-point methods, primal parallel trajectories method 93 Path-following interior-point methods, primal parallel trajectories method, efficiency estimate 96 99 Path-following interior-point methods, primal parallel trajectories method, scheme 95 Path-following scheme 2 57 Perturbed primal problem, cost function 106 Perturbed primal problem, properties of 106 Polynomial-time methods, definition for LP 3 Polynomial-time methods, definition for NLP 5 Polynomial-time methods, historical remarks 380 Positive-semidefinite representation 237 Positive-semidefinite representation of determinant 240 Positive-semidefinite representation of Euclidean norm 238 Positive-semidefinite representation of fractional-quadratic function 241 Positive-semidefinite representation of geometric mean 240 Positive-semidefinite representation of matrix norm 238 Positive-semidefinite representation of maximal eigenvalue 239 Positive-semidefinite representation of quadratic-functional 238 Positive-semidefinite representation of sum of k largest eigenvalues 239 Potential reduction interior-point methods 101 Potential reduction interior-point methods, anticipated behaviour 248 381 Potential reduction interior-point methods, Karmarkar method 111 Potential reduction interior-point methods, Karmarkar method, assumptions 111 Potential reduction interior-point methods, Karmarkar method, potential function for 112 Potential reduction interior-point methods, Karmarkar method, projective transformation-based explanation of 116 Potential reduction interior-point methods, Karmarkar method, rate of convergence 115 Potential reduction interior-point methods, Karmarkar method, scheme 114 Potential reduction interior-point methods, Karmarkar method, sliding objective approach 119 Potential reduction interior-point methods, Karmarkar method, unknown optimal value 117 Potential reduction interior-point methods, primal-dual method 138 Potential reduction interior-point methods, primal-dual method, assumptions 138 Potential reduction interior-point methods, primal-dual method, large-step strategy 145 Potential reduction interior-point methods, primal-dual method, potential function 139 Potential reduction interior-point methods, primal-dual method, rate of convergence 144 Potential reduction interior-point methods, primal-dual method, scheme 140 Potential reduction interior-point methods, projective method 121 Potential reduction interior-point methods, projective method, assumptions 121 123 Potential reduction interior-point methods, projective method, large-step strategy 135 Potential reduction interior-point methods, projective method, potential function 124 Potential reduction interior-point methods, projective method, rate of convergence 130 132 Potential reduction interior-point methods, projective method, scheme 126—130 Preconditioned conjugate gradients method 346 Problems, approximation in 232 Problems, arising in control theory 245 Problems, complementarity 277 381 Problems, conic involving second-order cone 223 Problems, geometrical programming 230 Problems, inscribing maximal ellipsoid into polytope 244 Problems, minimization of largest eigenvalue 242 Problems, minimization of matrix norm 234 242 Problems, quadratically constrained quadratic 220 241 381 Problems, quadratically constrained quadratic, path-following approach 220 Problems, quadratically constrained quadratic, potential-reduction approach 221 Problems, reducible to inequality with monotone operator 275 Problems, semidefinite programming 236 Pure exchange model of Arrow — Debreu 302 Recessive cone 45 Recessive subspace 15 Relative Lipschitz condition 383 Second-order representation 224 Second-order representation, Euclidean norm 226 Second-order representation, fractional-quadratic function 227 Second-order representation, geometrical mean 226 Second-order representation, quadratic functional 226 Self-concordance 12 Self-concordant barrier 3 Self-concordant barrier for cone of positive-semidefinite symmetric matrices 198 Self-concordant barrier for epigraph of entropy function 192 Self-concordant barrier for epigraph of exponent 193 Self-concordant barrier for epigraph of fractional-quadratic function 201 Self-concordant barrier for epigraph of functions of Euclidean norm 195 Self-concordant barrier for epigraph of logarithm 193 Self-concordant barrier for epigraph of matrix norm 199 Self-concordant barrier for epigraph of power function 191 192 Self-concordant barrier for piecewise-quadratically bounded domains 194 Self-concordant barrier for polytope 193 203 Self-concordant barrier for second-order cone 195 Self-concordant barrier, bounds on parameter 42 49 Self-concordant barrier, definition of 32 Self-concordant barrier, examples 33 40 81 Self-concordant barrier, Legendre transformation 45 47 86 Self-concordant barrier, main properties 33 34 39 Self-concordant barrier, parameter of 4 32 Self-concordant families 58 Self-concordant families, barrier-generated 66 Self-concordant families, center-generated 80 Self-concordant families, definition of 58 Self-concordant families, homogeneous 86 Self-concordant families, metric associated with 61 Self-concordant families, properties 58 59 62 Self-concordant function, behaviour on Lebesgue set 27—29 Self-concordant function, definition of 12 Self-concordant function, Legendre transformation 43 Self-concordant function, main properties 12 13 Self-concordant function, strongly 12 Self-concordant monotone operator, definition of 280 Self-concordant monotone operator, Newton decrement 284 Self-concordant monotone operator, Newton method 286 Self-concordant monotone operator, properties 280 282 283 285 Semidefinite programming 236 Standard logarithmic barrier 2 315 Symmetric k-linear form 361 Uniqueness theorem for linear differential equations 14 Universal barrier 49 Variational inequalities 273 Variational inequalities, accuracy measure 294 299 Variational inequalities, accuracy of approximation 298 Variational inequalities, application example 302 365 Variational inequalities, barrier-generated family of 294 Variational inequalities, path-following method for 290 Variational inequalities, path-following method for, efficiency estimate 302 Variational inequalities, path-following method for, initialization 296 Variational inequalities, path-following method for, summary 301 Variational inequalities, path-following method for, updating rule 295 Variational inequalities, reduction to convex program 305 Variational inequalities, regularity 305 Variational inequalities, with linear monotone operator 304 Volumetric barrier 203
Реклама
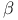-compatible with self-concordant barrier 
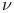-normal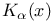 
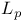-norm 
|
|
О проекте