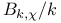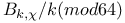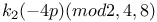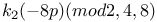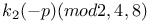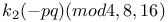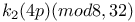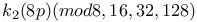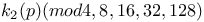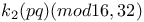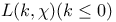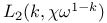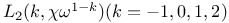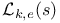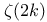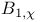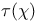|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Urbanowicz J., Williams K.S. Ч Congruences for L-Functions |
|
|
 |
| ѕредметный указатель |
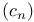 144 144
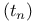 143 143
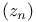 , , 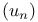 142 151 142 151
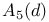 , , 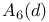 110 111 110 111
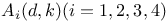 104 106 110 104 106 110
![$B^{[d]}_{m, \chi}$](/math_tex/15540b013421b931ad635d09a217a1d682.gif) 70 70
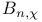 , nth generalized Bernoulli number 13 , nth generalized Bernoulli number 13
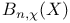 , nth generalized Bernoulli polynomial 14 , nth generalized Bernoulli polynomial 14
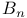 , nth Bernoulli number 9 , nth Bernoulli number 9
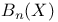 , nth Bernoulli polynomial 10 , nth Bernoulli polynomial 10
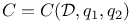 182 182
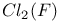 24 24
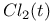 , Clausen function 20 , Clausen function 20
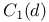 , , 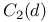 , , 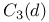 101 101
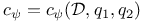 181 181
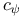 193 193
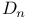 , nth D-number 13 , nth D-number 13
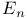 , nth Euler number 13 , nth Euler number 13
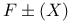 54 54
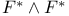 , modified external product 25 , modified external product 25
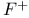 , maximal totally real subfield of F 23 , maximal totally real subfield of F 23
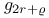 , , 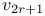 159 159
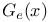 139 139
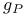 184 184
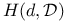 63 63
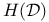 , , 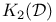 166 166
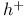 , , 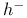 23 23
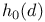 , number of narrow classes of , number of narrow classes of 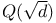 30 30
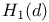 , , 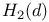 63 63
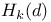 113 113
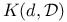 93 93
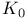 , , 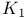 , , 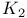 , Milnor K-functors 24 , Milnor K-functors 24
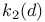 , order of the group , order of the group 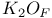 for for 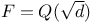 29 29
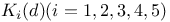 94 94
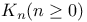 , Quillen K-functors 23 , Quillen K-functors 23
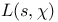 , Dirichlet L-function 16 , Dirichlet L-function 16
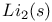 , Euler dilogarithm 19 , Euler dilogarithm 19
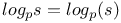 , p-adic logarithm 118 , p-adic logarithm 118
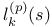 126 126
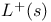 , , 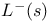 , , 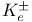 127 127
![$L^{[m, \Theta]}_{2}(k, \chi_{ed}\omega^{1-k})$](/math_tex/98637660d3f335ea7aaa837fa58ef50782.gif) 160 160
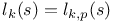 , kth p-adic multilogarithm 122 , kth p-adic multilogarithm 122
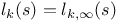 , kth complex multilogarithm 122 , kth complex multilogarithm 122
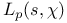 , p-adic L-function 119 , p-adic L-function 119
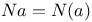 21 21
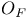 , ring of integers of a number field F 21 , ring of integers of a number field F 21
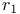 , , 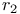 21 21
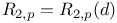 , second p-adic regulator of , second p-adic regulator of 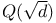 122 122
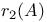 , Sylow 2-rank of a finite abelian group A 24 , Sylow 2-rank of a finite abelian group A 24
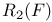 , second Borel regulator of F 26 , second Borel regulator of F 26
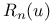 , nth Frobenius polynomial 14 , nth Frobenius polynomial 14
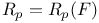 , p-adic regulator of F 121 , p-adic regulator of F 121
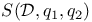 181 181
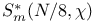 36 36
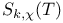 129 129
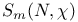 13 13
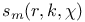 33 33
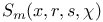 45 45
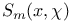 36 36
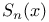 10 10
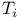 , (i = 1, 2, 3, 4) 108 , (i = 1, 2, 3, 4) 108
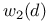 , , 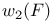 for for 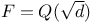 29 29
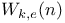 134 134
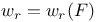 , largest integer s such that the group , largest integer s such that the group 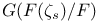 is annihilated by r 26 is annihilated by r 26
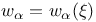 137 137
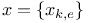 141 141
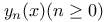 142 142
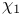 , trivial primitive character 2 , trivial primitive character 2
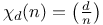 , Kronecker symbol 2 , Kronecker symbol 2
 , ,  97 97
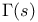 , Gamma function 11 , Gamma function 11
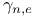 134 134
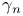 133 133
 , , 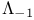 , , 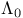 , , 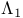 , , 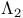 , , 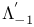 , , 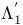 166 166
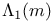 , , 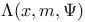 , , 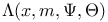 161 164 161 164
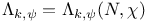 129 129
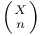 120 120
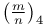 , biquadratic symbol 56 57 59 , biquadratic symbol 56 57 59
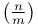 , Jacobi symbol 1 , Jacobi symbol 1
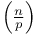 , Legendre symbol 1 , Legendre symbol 1
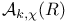 37 37
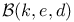 229 229
 181 181
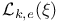 137 137
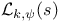 127 127
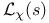 31 31
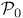 , , 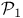 182 182
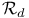 , , 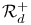 , , 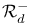 97 97
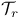 , set of all fundamental discriminants dividing r 69 , set of all fundamental discriminants dividing r 69
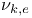 139 139
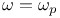 , Teichmueller character at p 119 , Teichmueller character at p 119
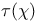 , normalized Gauss sum 9 , normalized Gauss sum 9
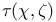 , Gauss sum 9 , Gauss sum 9
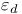 , , 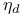 , , 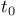 , , 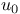 , t, u, T, U, , t, u, T, U,  171 171
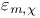 36 36
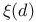 , , 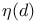 101 101
 , Riemann zeta function 11 , Riemann zeta function 11
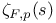 , p-adic zeta function 121 , p-adic zeta function 121
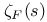 , Dedekind zeta function 21 , Dedekind zeta function 21
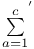 , sum taken over integers a prime to c 127 , sum taken over integers a prime to c 127
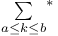 , if a or b is an integer, then the associated summands are halved 8 , if a or b is an integer, then the associated summands are halved 8
<a> 119
A(F), C(F), 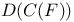 25 25
A(t, n), number of positive integers 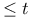 prime to n 48 prime to n 48
Akiyama, S. 32 231
Ambiguous forms and classes 30 51 55Ч56 62 74Ч75
Amice, Y. 119 231
Ankeny, N.C. 13 231
Apostol, T.M. 8 11 231
Ars Conjectandi 10
Artin, E. 13 231
Ayoub, R. 39 231
Barkan, P. 55 58Ч59 231
Barner, K. 27 231
Barrucand, P. 56 59 82 231
Bauer, H. 75 231
Belabas, K. 25 231
Berger, A. 13 231
Berger, R.I. 25 232
Berndt, B.C. 6Ч9 33Ч34 39Ч42 45 60 62 64 72 84 232
Bernoulli numbers 9 11Ч12
Bernoulli polynomials 10
Bernoulli, J. 10
Binomial coefficient identities 133 135 151
Birch, B.J. 26 232
Bloch, S. 20 26 232
Boldy, M.C. 25 232
Borel, A. 24 26 232
Borevich, Z.I. 3 10Ч12 19 21 28 30 72 232
Boulling, R. 6 232
Brauckman, B. 25 232
Browkin, J. 20 24Ч26 77 81 95Ч96 231Ч233
Brown, E. 55Ч56 58Ч59 61Ч62 74Ч75 82 84 233
c = c(y), exponent of 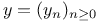 142 142
c(L) 143
Candiotti, A. 25 81 233
Carlitz, L. 10 14Ч15 124 233
Cauchy, A.L. 39 233
Character analogue of the Poisson formula 8 28Ч29 31 34
Chowla, S. 7Ч8 13 39 53 73 231Ч233
Cl(F), group of ideal classes of a number field F 24
Class number formulae 21 121
Clausen function 20
Clausen, T. 10 20
CM-fields 23
Coates, J. 27 119 233
Cohn, H. 56Ч57 59 82 231 233
Coleman formulae xi 122
Coleman, R.F. xi 64 122Ч123 125Ч126 132 140Ч141 234
Congruences for 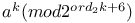 98Ч100 98Ч100
| Congruences for ![$B^{[T]}_{k, \chi}(N)/k$](/math_tex/c3b7889a54f0bb49aff98906f73f427282.gif) 217 220 217 220
Congruences for 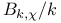 69 77 224 69 77 224
Congruences for 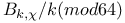 97 108 111Ч112 114Ч115 97 108 111Ч112 114Ч115
Congruences for 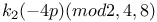 95 95
Congruences for 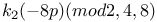 95Ч96 95Ч96
Congruences for 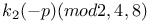 95 95
Congruences for 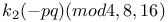 96 96
Congruences for 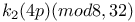 85 85
Congruences for 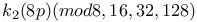 85 92 85 92
Congruences for 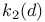 77 175 77 175
Congruences for  176 179 176 179
Congruences for  78Ч84 86 88 90Ч91 93 104Ч107 111Ч112 114Ч115 174 177 210 78Ч84 86 88 90Ч91 93 104Ч107 111Ч112 114Ч115 174 177 210
Congruences for 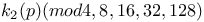 85 92 85 92
Congruences for 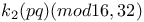 85 85
Congruences for 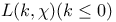 69 69
Congruences for 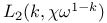 128 160 163 128 160 163
Congruences for 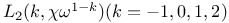 161 166 168 174Ч177 179 161 166 168 174Ч177 179
Congruences for 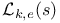 156 158 156 158
Congruences for h(-4p)(mod 4, 8, 16, 128) 55Ч59 65 92 170 172Ч173
Congruences for h(-4pq)(mod 8, 16) 61Ч62 65
Congruences for h(-4pqr)(mod 32) 68Ч69
Congruences for h(-8p)(mod 4, 8, 16, 128) 58Ч60 65 75 92 170 172
Congruences for h(-8pq)(mod 8, 16) 61Ч62 65
Congruences for h(-8pqr)(mod 32) 68Ч69
Congruences for h(-p)(mod 4, 8, 16, 128) 52 54 59 65 74 92 170 172
Congruences for h(-pq)(mod 4, 8, 16) 60Ч61 65
Congruences for h(-pqr)(mod 8, 32) 68
Congruences for h(4p)(mod 4, 8, 16) 54 74 170 172
Congruences for h(8p)(mod 4, 8, 16) 74Ч75 170 172
Congruences for h(d) 51 76 168Ч172
Congruences for h(d)(d<0) ix 52 63Ч64 78 80Ч81 86 88 90Ч91 93 97 104Ч107 111Ч112 114Ч115 174 179
Congruences for h(d)(d>0) 53 176Ч177
Congruences for h(p)(mod 4, 8, 16) 53 57Ч58 73 170 172Ч173
Congruences for h(pq)(mod 4, 8) 75
Congruences for h(pqr), h(4pq) and h(8pq) 75
Congruences for p-adic numbers 118
Congruences for power sums of consecutive natural numbers 222
Conjecture of Birch and Tate 26Ч27 29 78 81
Conjecture of Federer 27
Conjecture of Leopoldt 121
Conjecture of Lichtenbaum 26 30 165
Conner, P.E. 25 27 30 76 81 95Ч96 234
Cooke, G. 57 233
Costa, A. 63Ч64 234
Currie, J. 8 45 60 234
Cuspidal behaviour of 2-adic modular forms 64
D(s), dilogarithm of Wigner and Bloch 20
d, fundamental discriminant 2
D-numbers 13
Damey, P. 75 234
Davenport, H. 2 184 234
Dedekind zeta function 21
Dedekind, R. 41 55 234
Deligne, P. 119 234
Desnoux, P.-J. 76 167 234
Dilcher, K. 10 234
Dilogarithm of Euler 19
Dilogarithm of Rogers 20 125
Dilogarithm of Wigner and Bloch 20 26
Dirichlet characters 2 184
Dirichlet class number formulae x 2Ч4 16 21Ч22 27Ч28 40 53Ч54 58 72 198 203
Dirichlet L-functions 16 18 119Ч120
Dirichlet regulator 21
Dirichlet, P.G.L. 2Ч3 6 39Ч41 53 55 235Ч236
E = E(F), group of units in F 23
E*(x), R(x), R*(x) 34
Endo, A. 76 235
Ernvall, R. 13 15 235
Euler criterion 1
Euler factors 16 119Ч120 123
Euler formula for 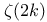 12 12
Euler numbers 13 115
Euler product 16
Euler, L. 12 19 235
Exact hexagon 76
Federer, L.J. 27 235
Fleckinger, V. 26 122 240
Formulae for 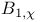 28 43 28 43
Formulae for 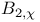 29 29
Formulae for 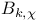 100 100
Formulae for  30 30
Formulae for  29 34 43 78Ч79 97 101 104 210 29 34 43 78Ч79 97 101 104 210
Formulae for 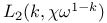 129 129
Formulae for 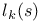 125 125
Formulae for 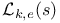 141 141
Formulae for 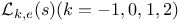 137 137
Formulae for 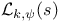 127Ч130 127Ч130
Formulae for h(d) 30
Formulae for h(d)(d<0) 2Ч3 5Ч6 27Ч28 33Ч34 39Ч41 43Ч44 79 101 103 183
Formulae for h(d)(d>0) 28
Fox, G.J. xi 77 203 207Ч208 235
Fresnel, J. 119 231 235
Friesen, C. 74 235
Frobenius polynomials 14 123Ч124
Frobenius, F.G. 14 122 235
Functional equation for 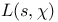 16 16
Functional equation for  11 11
Functional equation for 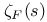 22 22
Fundamental discriminants 2
g(2) 24
Gamma function 11
Gangl, H. 25 231 233
Garland, H. 24 235
Gauss congruence 55Ч56 58Ч59 75 203 208
Gauss evaluation of 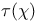 17 17
Gauss sum 9 17
Gauss theory of ambiguous classes 30 51 55 76
Gauss, C.F. 6 41 55Ч56 60 234 236
Gebhardt, H.M. 25 236
Generalized Bernoulli numbers 12Ч13 18 31 70 124 213
Generalized Bernoulli polynomials 13Ч14
Generalized Kummer congruences 15 97 119
Glaisher, J.W.L. 41 55 236
Goren, E.Z. 97 236
Gradshteyn, I.S. 36 236
Granville, A. 133Ч134 181
Gras, G. xЧxi 64 72 76 97 117 128 134 150 160Ч161 165 167 169 175 230 236
Greither, C. 27 236
h = h(F), class number of F 23
h(d), class number of 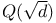 2 2
Halter-Koch, F. 76 236
Hardy Ч Williams congruence 62Ч64 68Ч69 93
Hardy, K. ix xi 6 49 51 61Ч64 71 75 128 165 167 169 174 236
Hasse classical Klassenzahlbericht 76
Hasse, H. 2 56 58 60 75Ч76 83Ч84 184 237
Hecke, E. 22 27 237
Hikita, M. 76 168 237
Holden, H. 3 6 40Ч41 45 237Ч238
Hudson, R.H. 3 6 44 238
Hurrelbrink, J. 25 27 30 63 76 81 95Ч96 234 238
Hurwitz, A. 13 41 54 238
Ireland, K. 3 10Ч12 16 238
Iwasawa, K. 12 119 238
Jacobi symbols 1
Johnson, W. 3 5 7 45 202 238
K-theorelic background 23
Kaplan, P. 56Ч58 61Ч62 75Ч76 168 172Ч173 236 238Ч239
Karpinski, L.C. 3 41 239
Kenku, M.A. 64 167 239
Keune, F. 24Ч25 239
Kisilevsky, H. 63 239
Kleboth, H. 13 239
Klingen, H. 27 239
Koblitz, N. 11 117 239
Koch, H. 76 239
Kohno, Y. 76 240
Kolster, M. 25Ч27 81 122 238 240
Kramer, K. 25 81 233
Kronecker symbols 2Ч3
Kronecker, L. 53 240
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



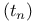
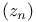 ,
, 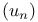
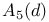 ,
, 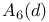
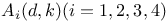
![$B^{[d]}_{m, \chi}$](/math_tex/15540b013421b931ad635d09a217a1d682.gif)
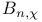 , nth generalized Bernoulli number
, nth generalized Bernoulli number 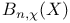 , nth generalized Bernoulli polynomial
, nth generalized Bernoulli polynomial 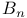 , nth Bernoulli number
, nth Bernoulli number 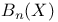 , nth Bernoulli polynomial
, nth Bernoulli polynomial 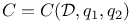
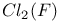
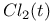 , Clausen function
, Clausen function 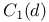 ,
, 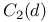 ,
, 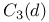
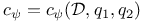
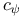
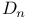 , nth D-number
, nth D-number 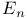 , nth Euler number
, nth Euler number 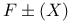
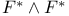 , modified external product
, modified external product 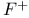 , maximal totally real subfield of F
, maximal totally real subfield of F 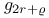 ,
, 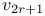
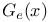
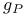
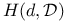
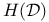 ,
, 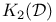
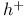 ,
, 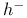
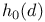 , number of narrow classes of
, number of narrow classes of 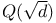
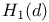 ,
, 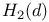
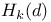
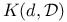
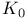 ,
, 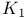 ,
, 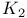 , Milnor K-functors
, Milnor K-functors 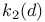 , order of the group
, order of the group 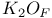 for
for 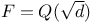
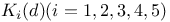
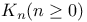 , Quillen K-functors
, Quillen K-functors 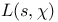 , Dirichlet L-function
, Dirichlet L-function 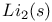 , Euler dilogarithm
, Euler dilogarithm 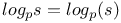 , p-adic logarithm
, p-adic logarithm 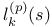
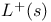 ,
, 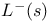 ,
, 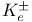
![$L^{[m, \Theta]}_{2}(k, \chi_{ed}\omega^{1-k})$](/math_tex/98637660d3f335ea7aaa837fa58ef50782.gif)
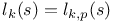 , kth p-adic multilogarithm
, kth p-adic multilogarithm 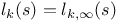 , kth complex multilogarithm
, kth complex multilogarithm 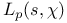 , p-adic L-function
, p-adic L-function 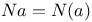
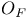 , ring of integers of a number field F
, ring of integers of a number field F 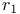 ,
, 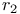
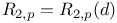 , second p-adic regulator of
, second p-adic regulator of 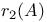 , Sylow 2-rank of a finite abelian group A
, Sylow 2-rank of a finite abelian group A 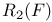 , second Borel regulator of F
, second Borel regulator of F 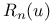 , nth Frobenius polynomial
, nth Frobenius polynomial 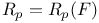 , p-adic regulator of F
, p-adic regulator of F 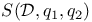
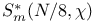
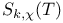
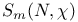
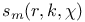
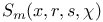
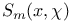
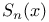
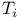 , (i = 1, 2, 3, 4)
, (i = 1, 2, 3, 4) 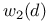 ,
, 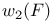 for
for 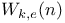
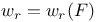 , largest integer s such that the group
, largest integer s such that the group 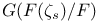 is annihilated by r
is annihilated by r 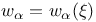
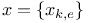
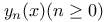
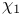 , trivial primitive character
, trivial primitive character 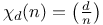 , Kronecker symbol
, Kronecker symbol  ,
, 
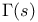 , Gamma function
, Gamma function 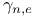
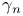
 ,
, 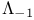 ,
, 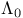 ,
, 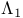 ,
, 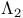 ,
, 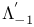 ,
, 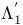
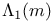 ,
, 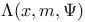 ,
, 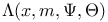
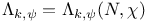
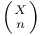
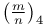 , biquadratic symbol
, biquadratic symbol 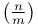 , Jacobi symbol
, Jacobi symbol 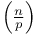 , Legendre symbol
, Legendre symbol 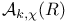
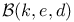

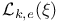
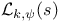
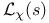
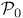 ,
, 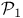
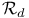 ,
, 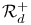 ,
, 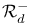
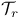 , set of all fundamental discriminants dividing r
, set of all fundamental discriminants dividing r 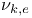
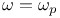 , Teichmueller character at p
, Teichmueller character at p 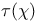 , normalized Gauss sum
, normalized Gauss sum 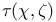 , Gauss sum
, Gauss sum 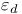 ,
, 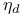 ,
, 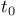 ,
, 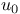 , t, u, T, U,
, t, u, T, U, 
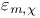
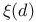 ,
, 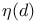
 , Riemann zeta function
, Riemann zeta function 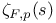 , p-adic zeta function
, p-adic zeta function 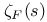 , Dedekind zeta function
, Dedekind zeta function 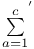 , sum taken over integers a prime to c
, sum taken over integers a prime to c 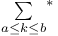 , if a or b is an integer, then the associated summands are halved
, if a or b is an integer, then the associated summands are halved 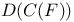
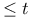 prime to n
prime to n 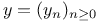
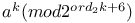
![$B^{[T]}_{k, \chi}(N)/k$](/math_tex/c3b7889a54f0bb49aff98906f73f427282.gif)