|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kollar J. — Rational curves on algebraic varieties |
|
|
 |
| Предметный указатель |
 294 294
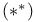 294 294
 , ,  160 160
 3 3
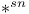 , , 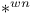 85 85
![$*^{[-1]}(\ )$](/math_tex/0dcf0896ca8199dc8bccfca9ee10ada582.gif) 46 46
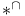 124 124
 , ,  17 17
 , , 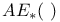 122 122
 , ,  119 119
 , ,  122 122
 , ,  51 74 51 74
 , ,  71 71
 , ,  71 71
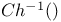 56 58 56 58
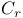 -field 230 -field 230
 , , 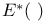 23 28 23 28
 78 78
 11 11
 , ,  9 9
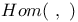 16 16
 94 94
 56 56
 , , 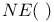 , ,  126 126
 123 123
 , ,  122 122
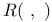 173 173
 , ,  108 108
 214 214
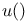 , , 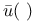 186 186
 , ,  121 121
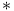 -negative extremal ray 127 -negative extremal ray 127
 210 210
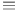 122 122
 240 240
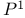 -bundle 105 -bundle 105
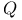 -Fano 240 -Fano 240
 , , 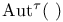 17 17
 18 123 18 123
 212 212
 166 166
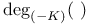 119 119
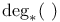 41 41
 11 11
 115 115
 111 111
 105 105
 109 109
 , ,  126 126
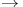 , ,  3 3
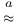 , ,  , ,  122 122
 , ,  123 123
Algebraic cycle 41
Algebraic equivalence 122
Algebraic realization 210
Algebraic relation 210
Ample (vector bundle) 116 265
Anticanonical degree 119
Attaching trees 155
Auticanonical degree 119
Auticanonical ring 173
Bend-and-break 134
Big 3
Birational transform 3
Canonical ring 173
Cayley form 56
CDiv( ) 17
ch( ) 56
Chain (of smooth rational curves) 155
Chow field 56
Chow field condition 70
Chow form 56
Chow functor 51 74
Chow pull-back 50 51
Chow( ) 52
Closed under 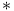 192 192
Comb 156
Cone of curves 126
Cone of effective cycles 122
Connected by a 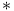 -chain 212 -chain 212
Connected by a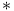 -chain (of smooth rational curves) 212 -chain (of smooth rational curves) 212
Contractible 134
Cycle theoretic fiber 45 46
Cycle, defined over a subfield 42
Cycle, theoretic fiber 45 46
Cyclic cover 149
Degree 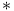 uniruling 181 uniruling 181
Degree (of a cycle) 41
Degree of a cycle 41
Del Pezzo surface 171
Del Pezzo, surface 171
DVR 3
Effective Cartier divisor 17
Effective cycle 41
Equivalence (algebraic, effective algebraic, effective rational, numerical, rational) 121—123
Equivalence relation 210
Equivalent (algebraically, rationally, numerically) 121—123
Essentially independent (family of cycles) 45
Essentially the same cycle 45
Exceptional set 286
Extremal ray 127
Extremal subcone 127
Fam( ) 119 123
Family of algebraic cycles 46
Family of rational curves 108
Family of rational curves through 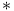 109 109
Fano variety 240
Fano variety of lines 266
Field condition 70
Field of definition 19
Finite type (property) 144
Flat pull back 41
Flat pull-back 41
Flat section 135
Free morphism 113
Free over 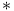 113 113
| Fundamental cycle 41
General deformation 115
General point 3
Generically unobstructed 33
Geometrically irreducible 108
Geometrically normal 79 108
Geometrically rational 103 199
Geometrically rational components 103
Geometrically reduced 79 108
Geometrically ruled 181
Geometrically smooth 103
Grassmann functor 11
Group scheme 17
Handle 156
Hilb( ),  10 74 10 74
Hilbert functor 9 74
Hilbert polynomial 9
Hom functor 16
Hom( , ) 16
Hom( , , ) 94
Incidence correspondence 53
Index (of a Fano variety) 245
Inseparably unirational 206
Inseparably uniruled 206
Intersection number 294 295
Irreducible algebraic relation 210
Irreducible relation 210
Line 248
Locally unobstructed 33
Locus 104 164
Locus( ) 104 164
MAP 3
Maximal rationally chain connected fibration 222
Maximal rationally connected fibration 223
Minimal (free morphism) 195
Minimal free 195
Mod 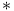 -reduction 144 -reduction 144
Morphism 3
MRC-fibration 223
MRCC-fibration 222
Nearby smoothable 154
Nef vector bundle 265
nef, 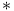 -nef 124 -nef 124
Nonnegative cycle 41
Normal form 211
Normal point 79
Normic form 230
Numerical equivalence 123
Obs( ) 29
Obstruction 23 28
Obstruction space 29
Obtained from 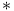 by attaching trees 155 by attaching trees 155
Open algebraic relation 210
Open relation 210
Picard number 126
Prerelation 212
Prime divisor (of a field) 286
Proalgebraic relation 210
Product (of algebraic relations) 210
Product (of relations) 209
Proper algebraic relation 210
Proper relation 210
Push forward 41 81
Quot scheme 77
Quot( , ), 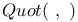 77 77
rational 103 198
Rational equivalence 122
Rationally chain (of smooth rational curves) connected 199
Rationally chain connected 199
Rationally chain connected fibration 222
Rationally connected 199
RatLocus( ) 104
Reduced point 79
Relation 209
Relation class 210 212
Relative Cartier divisor 17
Represent (a functor) 8
Root, 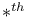 root of root of 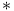 149 149
Ruled 181
Ruled modification 289
S*( ) 10
Semi normal 84
Semi normalization 84
Semi positive (vector bundle) 116
Separably rationally connected 199
Separably ruled 181
Separably unirational 199
Separably uniruled 181
Seshadri constant 305
Set theoretically equivalent 210
Smooth point 79
Smoothable 98 154
Smoothable fixing 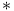 154 154
Subcomb 156
Supporting function 127
Tooth 156
TREE 155
Two general points can be connected by a  -chain 213 -chain 213
Unirational 199
Uniruled 181
Uniruled modification 289
Uniruled with curves of 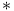 -degree -degree 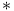 183 183
Univ( ),  10 52 10 52
Universal element 9
Universal family 9
Unobstructed 30
Unsplit (family of morphisms or rational curves ) 192
Unsplit family of rational curves 192
Very general point 3
WDiv( ) 123
Weak normalization 84
Weakly normal 84
Weighted projective space 240
Well defined family of algebraic cycles 46 47
Well formed (weighted projective space) 240
[] 41
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




 ,
, 

 ,
, 
![$*^{[-1]}(\ )$](/math_tex/0dcf0896ca8199dc8bccfca9ee10ada582.gif)
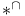
 ,
, 
 ,
, 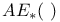
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ,
, 
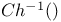
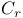 -field
-field  ,
, 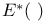


 ,
, 
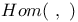


 ,
, 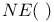 ,
, 

 ,
, 
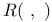
 ,
, 

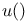 ,
, 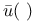
 ,
, 
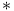 -negative extremal ray
-negative extremal ray 
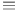

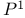 -bundle
-bundle 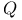 -Fano
-Fano  ,
, 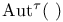



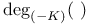
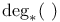





 ,
, 
 ,
, 
 ,
,  ,
, 
 ,
, 

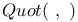
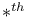 root of
root of  -chain
-chain