|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| McEliece R.J. — Finite Fields for Computer Scientists and Engineers |
|
|
 |
| Предметный указатель |
Antilogarithxns 27
Associate 13 17
Autocorrelation function 156 167
Basis, dual 110
Berlekamp's bit serial multiplication circuits 110ff
Berlekamp's polynomial factorization algorithm 84ff
Binomial coefficients 44 146
Binomial theorem 45 52
Blumer, A. 119
Calculus, freshman 57
Characteristic equation, of linear recursion 124
Chevalley — Warning, Theorem of 182
complex numbers 23 24 70 76
Conjugates 46
Correlation, between two sequences 155
Crosscorrelation function 171—172
Crosstalk 170
Cyclotomic cosets 91
Cyclotomic polynomials 76ff
Decimal, repeating 53
Decimation 162
Degree, of an element in a finite field 47
Derivative, formal 57 72
Distribution problems 137ff
Division algorithm 24
Division, synthetic 24 93
Divisor, proper 14
Domain, integral 3
Euclid 3
Euclid's algorithm, could be taught to junior high school students 6
Euclid's algorithm, extended version of 9
Euclid's algorithm, statement of 7
Euclidean domain, defintion of 3
Euclidean domain, examples of 4
Euler Product technique 58
Euler's  function, definition of 33 function, definition of 33
Euler's  function, formulas for 65 function, formulas for 65
Fact, a curious 7 12
Factorization, trivial 13 17
Factorization, unique factorization theorem 15
Fibonacci numbers 7 11 123—125 131 138 141 142 149
Field with four elements 1
Field with one element 2
Field with p elements 1 22
Field, characteristic of 30
Field, definition of 1
Field, finite, existence of 67
Field, infinite are uninteresting 1
Field, uniqueness of 69
Gauss's algorithm for finding primitive roots 38 52
Gaussian integers 4 10 14 17 28
GCD see "Greatest common divisor"
Generating functions 58
Gold sequences 196 200
Greatest common divisor, computationally clumsy algorithm for finding 16
Greatest common divisor, definition of 4
| Greatest common divisor, expressed as a linear combination of things 5
Hilbert's algorithm for solving 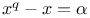 104ff 104ff
Initial conditions, for linear recurrence relation 123
Junior high school algorithm for finding gcd's 16
Kloosterman sum 174
Lagrange's theorem 31
Linear recurrences 123ff
Linear recurrences, characteristic polynomial 127
Linear recurrences, cycles in equivalent solutions to 134
Linear recurrences, cyclic equivalence of solutions to 132
Logarithms 27
m-gram 152
M-sequences 151ff
m-sequences, canonical cyclic shift of 160
m-sequences, crosscorrelation between two, Big Theorem about 193
m-sequences, cycle-and-add property of 159
m-sequences, number of different 161
m-sequences, run-distribution properties of 154
Maximal-length shift register sequences see "m-sequences"
Moebius function 62ff
Moebius inversion 60ff
Norm, definition of 97
Norm, great, lesser, and relative 100
Odd crosscorrelation function 172
Order, of an element in a finite field 31
Parity tree 113
Period, reduced, of a sequence 137
PN sequences see "m-sequences"
Polynomials in several variables 182
Polynomials, characteristic, with repeated roots 145 149
Polynomials, interpolation 182
Polynomials, irreducible 14
Polynomials, minimal 41ff
Polynomials, number of irreducible of degree d 57 66
Polynomials, period of 130
Polynomials, primitive 43 151
Polynomials, reciprocal, coefficients of 94
Prime, in Euclidean domain 13
Prime, relatively 14
Primitive element 112n.
Primitive root 37
Primitive root, mod n 83
Projective cyclic equivalence 134.
Pseudo randomness properties, of m-sequences 152ff
Quadratic equations, solution of in characteristic 2 105ff
Quadratic forms 179ff
Quadratic forms, nonsingular 179
Quadratic forms, rank of 185
Quadratic forms, representing zero 179
Signature sequences, used in multi-user communication 169
Subfield 30 70
Trace, definition of 97
Trace, great, lesser and relative 100
Unit, in a Euclidean domain 13 17
Vandermonde matrix 140
Whiting, D. 118
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 function, definition of
function, definition of