Авторизация
Поиск по указателям
Greiner W., Neise L., Stöcker H. — Thermodynamics and statistical mechanics
Обсудите книгу на научном форуме Нашли опечатку?
Название: Thermodynamics and statistical mechanicsАвторы: Greiner W., Neise L., Stöcker H.Аннотация: The series of texts Classical Theoretical Physics is based on the highly successful series of courses given by Walter Greiner and his colleagues at the Johann Wolfgang Goethe University in Frankfurt am Main, Germany. Intended for advanced undergraduates and beginning graduate students, the volumes in this series will provide not only a complete survey of classical theoretical physics but also an enormous number of worked examples and problems to show students clearly how to apply the underlying principles to realistic problems.
Thermodynamics and Statistical Physics covers: Thermodynamics - basic definitions of thermodynamics, equilibrium, state variables - the first and second laws - phase transitions and chemical reactions - thermodynamic potentials Statistical Mechanics - statistics of microscopic states and connection to the entropy - the microcanonical, canonical and grand canonical ensembles - applications of Boltzmann statistics Quantum Statistics - the density operator - many-particle wave functions - ideal quantum systems - the ideal Bose gas and applications to blackbody radiation, Kirchhoff's law, and lattice vibrations - the ideal Fermi gas and applications to condensed-matter physics, astrophysics, and nuclear physics - relativistic Bose and Fermi gases and applications to particle physics Real Gases and Phase Transitions - real gases and the virial expansion - classification of phase transitions and critical indices - the Ising and Heisenberg models
FROM THE REVIEWS:
AUSTRALIAN & NEW ZEALAND PHYSICIST "As one might expect, it contains a thorough and complete coverage of a wide range of topics...It contains a wealth of worked examples: for instance, the theory of relativistic gases is illustrated by its application to one of Greiner's favorite topics, the quark-gluon plasma in the Big Bang and in heavy-ion collisions. It deserves serious consideration as a textbook for third-year courses in this area."
Язык: Рубрика: Физика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1995Количество страниц: 480Добавлена в каталог: 17.11.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
387 387 387 387 218 43 235 191 130 387 386 387 387 387 344 420 344 324 324 324 3K background radiation 332 Absorptivity 328 Adiabates 36 Antiferromagnetic materials 429 asymptotic freedom 387 Atomic mass 13 Avogadro’s number 13 Bag pressure 388 BCS theory 434 Bessel functions 234 big bang 3 Black holes 359 Bloch walls 425 blue 386 Boiling, delayed 70 Boltzmann 43 Boltzmann factor 164 Boltzmann statistics 208 Boltzmann’s constant 128 Boltzmann’s constant of proportionality 9 Bose condensation 318 Bose gas 314 Bose gas, Ultrarelativistic 325 Bose — Einstein statistics 292 Bosons 287 Bragg — Williams approximation 454 Braun — Le Chatelier principle 119 Brillouin function 219 451 Calorie 16 Calvalieri’s theorem 126 Canonical density matrix for 278 Canonical density operator 270 canonical ensemble 159 200 Canonical ensemble, harmonic oscillators in 169 Canonical ensemble, ideal gas in 166 Canonical ensembles, connection between microcanonical and 186 Canonical partition function 162 301 Canonical partition functions, weighted sum of 245 Canonical phase-space density 160 Carnot cycle 39 Carnot’s process 37 Chandrasekhar limit 361 chemical potential 13 15 Chemical reactions 62 Clausius 33 Clausius — Clapeyron equation 64 65 423 Clausius’ virial 197 Cluster 407 Cluster expansions 414 Coefficient of expansion 23 Coefficients, stoichiometric 63 Coherent 264 Color field 387 Color flux tube 387 Compressibility 23 Condensation of corresponding phonons 431 Condensation, delayed 70 confinement 387 Cooper pair 433 Coordinate representation 275 Copper, specific heat of 350 Critical indices 424 Critical point 69 Crystal structure, rearrangements of 431 Curie’s constant 217 Curie’s law 217 Cylinder functions 234 Davy 16 de Haas-van Alphen effect 371 374 Debye function 338 Debye temperature 338 Degeneration factor 187 Degrees of freedom, internal 225 Density matrix 280 Density matrix, properties of 265 Density of particles 178 Density of states 258 Density of states, one-particle 315 Density operator 260 Density operators 257 269 Differentials, exact 25 29 Differentials, inexact 25 29 Dipole moment, total mean 216 Dirac brackets 268 Dirac’s notation 261 Dulong and Petit, law of 21 Dulong and Petit, rule of 337 Efficiency 40 Einstein and Debye model 334 Einstein function 336 Endergonic 102 Endothermal 100 Energy gap 433 Energy hypersurface 126 Energy, Compressional 397 Energy, internal 33 34 Engines, thermodynamic 52 Ensemble average 143 177 Ensemble theory 123 142 Enthalpy 95 entropy 37 Entropy 39 Entropy 123 Entropy, as an ensemble average 149 Entropy, microscopic interpretation of 43 Entropy, statistical definition of 127 Equal distribution theorem 198 Equation of state for a real gas 17 Equations, adiabatic 35 Equations, of state 3 Equilibrium 3 Equilibrium state 6 Equilibrium, global 7 Equilibrium, global and local 51 Equilibrium, local thermal 7 Equipartition theorem 194 198 Ergodic hypothesis 142 144 Euler angles 226 Euler — Maclaurin formula 368 Euler’s equation 58 59 Exergonic 102 Exothermal 100 Expansion, isothermal 23 Fermi gas 341 347 Fermi gas, degenerate 347 350 Fermi gas, relativistic 355 Fermi gas, specific heat of 349 Fermi gas, ultrarelativistic 378 Fermi gases, applications of 386 Fermi — Dirac statistics 292 fermions 287 Ferrimagnets 429 Ferroelectric materials 430 Flavors 387 Fluctuations 45 191 248 Fock space 272 Free electron 264 Free energy 91 Free energy of ideal gas 94 Free enthalpy 101 Free particle 273 275 Free particle, calculation of 277 Free particles, canonical density matrix for 278 Fugacity 245 Fundamental relation 41 Gas constant 17 Gas, evaporating 174 Gas, ideal 9 Gas, ultrarelativistic 152 168 Gay — Lussac 9 Geometric distribution 310 Gibbs correction factor, general foundation of 164 Gibbs — Duhem relation 58 59 416 Gibbs — Helmholtz equation 103 Gibbs’ correction factor 133 Gibbs’ free enthalpy 248 Gibbs’ paradox 131 133 Gibbs’ phase rule 62 63 416 Gibbs’ phase rule, extended 64 Gibbs’ potential 101 Gluons 386 387 Grand canonical density operator 272 Grand canonical description 297 grand canonical ensemble 240 Grand canonical partition function 272 301 Grand canonical potential 273 Grand potential 107 Green 386 gyromagnetic ratio 218 Hadronic gas 396 Hallwachs effect 353 Hamiltonian 128 Hankel functions, first kind 234 Hankel functions, second kind 234 harmonic oscillator 280 Harmonic oscillators 156 Harmonic oscillators, 209 Heat 15 Heat bath 23 Heat capacities 110 heat capacity 15 Heat capacity, total 16 Heat, evaporation 417 Heat, latent 417 Heat, molar specific 17 Heat, reduced 39 Heaviside — Lorentz 385 Heavy-ion collisions 386 396 Heisenberg model, in mean-field approximation 450 Heisenberg, model of 436 Helmholtz potential 91 Henry and Dalton, law of 77 Hilbert space 261 Homogeneous functions of first order 59 Hydrodynamics 251 Ideal gas 171 188 293 314 341 Ideal gas law 9 Ideal gas, 179 Ideal gas, chemical potential of 60 Ideal gas, enthalpy of 97 Ideal gas, entropy of 86 Ideal gas, equations of state of the 139 Ideal gas, Euler’s equation for 60 Ideal gas, free enthalpy of 102 Ideal gas, kinetic theory of the 10 Ideal gas, partition function of the ultrarelativistic 236 Ideal gas, relative momenta in 181 Ideal gas, relativistic 233 Ideal gas, statistical calculation of the entropy of the 129 Ideal gas, virial theorem and 199 Ideal Quantum Systems 297 Incoherent 264 Integrating factor 28 Intensive state quantities 42 inversion 224 Irial expansion 414 Isentropes 36 Ising model 436 Ising model, in mean-field approximation 443 Ising model, in one dimension 438 Ising model, order-disorder phase transitions in 453 Isochoric 35 Jacobi determinant 116 Jacobi transformations 115 Joule — Thomson coefficient 118 Joule — Thomson experiment 112 Kelvin 385 Kirchhoff’s law 328 Kirchhoff’s law, derivation of 334 Landau 417 Landau diamagnetism 366 Landau diamagnetism, state density of 374 Lande factor 218 Langevin function 216 Law of atmospheres 180 Law of mass action 70 72 Law, first 33 Lee 420 Legendre transformation 87 Lennard — Jones potential 403 Linde’s liquefaction process 115 Line integrals 25 Liouville equation 267 Liouville’s theorem 145 146 Liquid crystals 432 London F. 324 Longitudinal waves 336 Macrocanonical distribution 242 Macrocanonical ensemble 240 248 Macrocanonical ensemble, ideal gas in 246 Macrocanonical partition function 244 Macrocanonical potential 245 Macroscopic quantum effects, superconductivity and superfluidity 433 Magnetic moment, total mean 219 Magnetization, spontaneous 453 Magnons 446 Maxwell construction 67 68 Maxwell relations 108 110 Maxwell — Boltzmann statistics 187 292 Maxwell’s velocity distribution 11 Mayer 414 Mayer, R.J. 15 Mayer’s cluster expansion 404 Mean occupation number 306 Mean occupation numbers, derivation of 310 Mean value 142 192 Mean value of all possible distributions, canonical ensemble as 200 Mean-field approximation 392 Meissner — Ochsenfeld effect 366 434 Microcanonical case 270 microcanonical ensemble 142 143 146 Microstate 44 124 Microstates 123 Microstates in a simple system 46 Minimum energy 84 MIT bag model 387 Mixed state 261 Mixing entropy 132 Molar fraction 13 Molecular field approximation 392
Реклама
 |
|
О проекте
|
|
О проекте



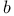 (beauty)
(beauty) 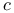 (charm)
(charm) 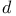 (down)
(down) 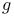 -factors
-factors 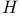 -Theorem
-Theorem 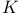 -functions
-functions 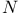 harmonic oscillators, density of states for
harmonic oscillators, density of states for 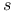 (strange)
(strange) 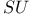 (3)
(3) 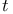 (top)
(top) 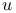 (up)
(up)  -function
-function  -transitions
-transitions  -function
-function 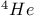 ,
, 
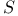
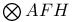
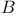 for
for 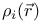 for
for 
 , number of
, number of