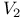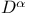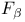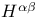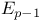|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Schouten J.A. — Tensor Analysis for Physicists |
|
|
 |
| Предметный указатель |
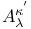 , , 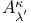 1 1
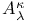 61 115 61 115
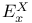 (v. Dantzig) 252 257 (v. Dantzig) 252 257
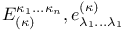 28 28
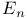 2 111 2 111
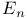 , centred 3 , centred 3
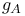 1 115 1 115
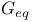 3 115 3 115
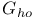 3 115 3 115
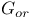 3 116 3 116
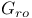 4 116 4 116
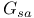 3 115 3 115
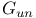 42 244 42 244
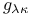 , , 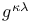 91 92 91 92
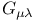 100 123 100 123
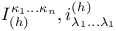 38 117 38 117
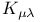 100 13 100 13
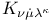 99 99
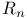 111 111
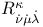 98 122 98 122
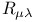 100 123 100 123
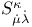 87 121 87 121
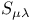 139 139
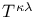 , , 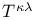 142 142
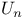 42 240 42 240
 91 91
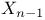 -building covariant vector fields 64 -building covariant vector fields 64
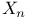 59 110 59 110
![$[\mathfrak{L}]$](/math_tex/6b7cd0e95e227a9370a8e4354c4e780782.gif) 79 79
 84ff 121 84ff 121
 -density 29 113 -density 29 113
 -function 251 -function 251
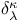 , , 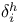 , , 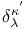 14 19 61 14 19 61
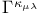 85 121 123 85 121 123
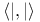 251 251
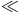 172 172
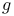 39 92 117 39 92 117
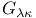 101 123 229 101 123 229
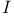 39 39
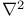 104 104
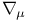 65 66 86ff 121 65 66 86ff 121
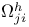 82 121 144 82 121 144
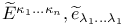 29 115 29 115
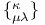 92 122 92 122
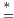 15 15
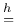 103 103
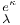 , , 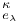 12 61 12 61
Absolute dimension 127 130ff
Absolute invariant 78 119
Addition 19 113
Affine geometry 2
Affine group 1
Affine space 2
Affinor 17 112
Allowable coordinate systems 2 59
Allowable systems of fundamental units 126
Alternating product 113
Alternation 20 113
angle 39 117
Anholonomic components 81
Anholonomic coordinate systems 81 102 123 194
Anholonomic mechanical systems 194
Antilinear transformation 249
Antisymmetric tensor 23
Axial bivector 52
Axial vector 52f
Basic bra 266
Bianchi, identity of 100 123
Bibliography 268
Birkhoff, G.D. 190
Bivector 54 56
Bivector-tensor 99
Bose statistics 254
Boundary value problems 106 124
Bra 243 250ff
Brandt, L. 9 59
Brillouin, L. 9 59 139 169
Brinkman, H.W. 239
Burkhardt, H. 103
Cady, W.G. 139 147 152 164 169 179 180 187
Cartesian coordinate systems 37
Cayley’s matrix calculus 40
Centre 3
Centred 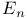 3 111 3 111
Christoffel symbol 92 102
Christoffel, L.B. 169
Commuting operators 247
Commuting set 259
Complete set of eigenkets (bras) 248 256
Conservation of momentum and energy 227
Contraction 19
Contravariant 9
Coordinate transformations 2
Coordinate-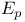 ’s 6 ’s 6
Coordinates, allowable 2 59
Coordinates, curvilinear 59 110
Coordinates, rectilinear 1 111
Coupling constants 184
Covariant vector 10
Crystal classes 152ff
Curvature affinor 98f 103 122f
Curvature of 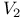 102 102
Curvature of  94ff 94ff
Curvilinear coordinates 59 110
D, 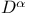 131 133 215 131 133 215
Dead indices 13 113
Decomposition of p-vector into blades 27
Definite, positive, negative 35 242
Deformation 139
densities 31 13
Derived units 126
Deviator 156
Diagonal matrix 262f
Dimension of domain 12 112
Dirac, P.A.M. 197 240 243 247 250 252 253 255 256 259 263 265 266 267
Direction 5
Displacement 84
div 67 118
Div, divergence 66 118
Divergence, principal theorem of 73
Domain with respect to an index 21
Domain, contravariant, covariant 12 112
Dorgelo, H. 29 45 127 131
Duration 37 91
Duschek, A. 40
Ecart geodesique 193
Eddington, A.S. 214
Effect, linear 160
Eiconal functions 202 203
Eigenket (bra) 246 254
Eigenstate 256
Eigenvalue 42 115 254 256
Eigenvector 43 115
Einstein convention 1
Einstein space 229 239
Einstein, A. 214
Eisenhart, L.P. 9 19 59 84 91
Elastic coefficients, adiabatic 144
Elastic coefficients, element of world lino 201
Elastic coefficients, elementary divisors 34
Elastic coefficients, isothermal 145
Emde, F. 105
Enantiomorphous 155
Energy function 174 178
Equiscalar 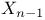 's 65 's 65
Equivoluminar 3
Euler 210
Eulerian angles 211
F, 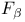 131 133 135 131 133 135
Fair, J.E. 164 185 187
| Fermi statistics 254
Field in 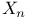 60 60
Field invariant for point transformations 75
Field of physical objects 127
Film-space 193
First integral 205 207
Fixed indices 2 110
Fokker, A. 171 214
Four-dimensional velocity vector 218 222
Free indices 19
Fresnel equations 177
Functions in involution 206
Functions of observables 257ff
Fundamental tensor 36 42 91 92 117 242
Fundamental units 126
Galilei group 220
Gauss, equation of 193
Gauss, theorem of 70
Generating set of transformations 153
Geodesic 88 122
Geometric image 127 130ff
Geometric object, quantity 9 60 112
Giorgi, system of 131
Givens, J.W. 24 40 45 58
Grad, gradient 64 118
Gravitation 229ff
Green’s function 107 125
Green’s identities 104 123f
Green’s medium 176
Green’s Theorem 105 124
Group 1
H, 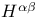 131 133 215 131 133 215
Hamel, G. 195 197
Hamilton — Jacobi equations 203
Hamiltonian equation 198 201
Hamiltonian function 198
Hamiltonian relation 200
Hermitian bivector 241
Hermitian tensor 241
Horak, Z. 194
Hybrid quantities 241
Hyperplane, coordinates 6
Identifications after introduction of screw sense 46
Identifications for 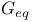 45 116 45 116
Identifications for 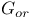 46 116 117 46 116 117
Identifications for 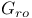 47ff 116 117 47ff 116 117
Identities of the curvature affinor 99 123
Identity of Bianchi 100 123
Improper 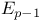 5 5
Incompressible fluid in 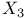 72 72
indefinite 35 242
INDEX 35 114
indices 1
Indices, dead, living 13
Indices, running, fixed 2 110
Indices, saturated, free 19
Intermediate components 17 110
Intersection 5
Interval functions 251
Inverse 1 18
Isomer 20 113
Jahnke, E. 105
Jordan, P. 240
Junction 6
K 100 123
Kasner, E. 239
Kernel letter 2 110
Kernel-index method 2
Ket 243 250ff
Klein, principle of 4
Koga, I. 177
Kramers, H. 240
Kronecker, L. 103 105
Kronocker symbols 14 19 61
Lack, F.K. 164 185 187
Lagrange 210
Lagrange derivative 78ff 120 123
Lagrange equation 80 198 200
Leibniz, rule of 77
Length 37 91 117 252
Levi Civita, T. 5 59 84
Lichnerowicz, A. 1 9
Lie derivative 76ff 114
Lie differential 74ff 119
Linear displacement 85 121
Lowering of indices 38
Mason, W.P. 142 147 164 179 180
Matrices and quantities of valence two 33 114
Matrix calculus in 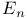 and and 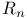 39 117 39 117
Matter density 225
Maupertuis equation 210
Mean energy density 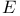 230 230
Mean energy-current density 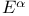 231 231
Mean momentum-current density 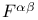 231 231
Mean particle current density 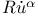 230 230
Measuring vectors 12 61
Meet 5
Meyer, W.F. 103
Michal, A.D. 9
Michelson — Morley experiment 218
Minkowski geometry 216
Minor 1
Mitschleppen 75
Mixed affinor 17 112
Mixed product 113
Mixing 20 113
Momentum-energy tensor density 225f
Momentum-energy vector 223
Multiplication 19 113
Multiplication of matrices 39
Multivector 23ff 113
n-vectors 28
nabla 86
Natural derivative 64 66 118
Natural parameter 89 122
Neumann, principle of 156
Newton’s gravitational constant 288
Nonor 157
Norm 243
Normal coordinates 89ff 122
Normal forms of bivector 35
Normal forms of tensor of valence two 34
Normalizing eigenkets (bras) to r, to  255 257 255 257
Null cone 37 117
Null curve 91 94
Null direction 91
Null form 4
Null manifold 4
Null vector 3 24 37 91 117
Object of anholonomity 82 120
Object transformations 9
Observable 256
Orientation 3 7 112
Oriented 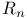 4 4
Oriented centred 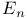 3 3
Origin 3
Orthogonal normal forms 42
Orthogonal transformation 3
Orthogonality (kots and bras) 252
Ostrogradski, theorem of 70
parallel 5
Parallelepiped 25
Parallelogram of forces 10
Parallelotope 25
Parametric form 5
Particle density 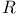 91 230 91 230
Pauli, W. 214 239
Perfect fluid 237
Perfectly perfect fluid 239
Phase factor 243 255
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



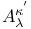 ,
, 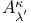
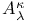
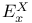 (v. Dantzig)
(v. Dantzig) 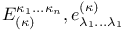
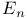
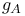
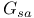
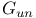
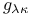 ,
, 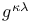
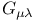
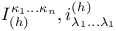
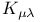
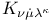
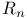
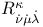
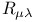
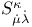
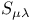
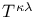 ,
, 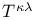
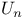

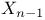 -building covariant vector fields
-building covariant vector fields 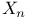
![$[\mathfrak{L}]$](/math_tex/6b7cd0e95e227a9370a8e4354c4e780782.gif)

 -function
-function 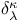 ,
, 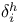 ,
, 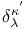
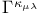
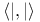
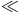
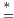
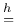
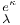 ,
, 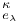
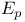 ’s
’s