|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Calogero F. — Variable phase approach to potential scattering |
|
|
 |
| Предметный указатель |
Allis, W. P. 1 20 236
Amplitude function 31ff 116ff 127 130
Analyticity properties of scattering parameters, as functions of angular momentum 2 235
Analyticity properties of scattering parameters, as functions of energy 2 143ff 235
Analyticity properties of scattering parameters, as functions of potential strength 100
Antibound state 156 159 233ff
Antivirtual state 156 159 233ff
Asymptotic convergence of pole functions 171ff
Babikov, V. V. 238
Bailey, P. B. 238
Bargmann, V. 182 183 184 237
Bellman, R. E. 205 207 237 238
Bergmann, O. 2 236
Bertocchi, L. 219(49) 237
Beyer, W. A. 239
Bonham, R. A. 2(9) 236
Born approximation 43ff 53ff 77ff 216
Bound states 143ff
Bounds on energies of bound states 195ff
Bounds on energy derivative of phase shift 38ff
Bounds on number of bound states 182ff
Bounds on scattering length 70ff
Bounds on scattering phase shift 37ff 51ff
Bounds on zero-energy cross section 70ff
Bromwich, T. J. 201(46) 237
Brownell, J. H. 184(44) 237
Brysk, H. 238
Buchanan, M. L. 238
Calogero, F. 2(13 14 15 16 17 18 19 24 25) 37(13) 92(13 16) 97(19) 98(19) 108(19) 109(19) 113(15 17) 115(17) 116(17) 119(17) 120(15 17 25) 125(15) 129(18) 173(13) 176(37) 182(38-41) 183(41) 185(41) 187(40) 189(38 39) 217(13) 222(13) 236 237
Chadan, K. 2(26) 41(30) 236
Charap, J. M. 2(25) 120(25) 236
Cohn, J. H. E. 239
Comparison functions 86 114
Condition for existence of bound states 187 189ff
Cosenza, G. 239
Cotangent function 17
Courant, R. 1 236
Cox, J. R. 2(22) 2(23) 140 141(22 23) 236
Cross section, absorption 133
Cross section, differential 3 121
Cross section, total 70ff
Curtiss, C. F. 238
Dashen, R. F. 2(11) 236 238
de Alfaro, V. 234(52) 237
Degasperis, A. 2(20) 136 236
Dirac equation 98 120
Drukarev, G. F. 2(3) 236
Eigenphase function 140ff
Eigenphase shift 139ff
Extremum principle for first-order differential equations 205ff
Extremum principle for scattering phase shift 50 57 93ff
Ferreira, E. M. 154(36) 235(36) 236
Feshbach, H. 202 237
Fivel, D. I. 239
Fl gge, S. 238 gge, S. 238
Fonda, L. 239
Franchetti, S. 2(7) 236
Fubini, S. 219(49) 237
Furlan, G. 219(49) 237
Ghirardi, G. C. 239
Glauber, R. G. 46 236
Guenn gu gu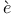 s, J. Y. 2(26) 236 s, J. Y. 2(26) 236
High-energy behavior of scattering phase shift 6 105ff 108 125 215ff 239
Hilbert, D. 1 236
Improved Born approximation 46 54ff 77ff
Interpolating functions 12
Jagannathan, G. 176(37) 237
Jost function 35
Kalaba, R. E. 45 236 238
Kane, J. 238
Karle, J. 2(9) 236
Keller, J. B. 2(10) 67 68(10) 181 236
Klar, H. 238
Klein — Gordon equation 98
Klein, A. 239
Kolodner, I. I. 201 238
Kouri, D. J. 238
Kr uger, H. 238 uger, H. 238
Kynch, G. J. 2(5) 120(5) 236
Levinson, N. 19(27) 71(27) 176 236
Levinson’s theorem 19 21 71 147 150 153 157 160 176ff 228
| Levy, B. R. 2(10) 67 68(10) 181 236
Limi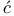 , N. 219(50) 237 , N. 219(50) 237
Low-energy behavior of scattering phase shift 67ff 109
May, R. M. 238
McKellar, B. H. J. 238
Mixing parameter 139ff
Mixing parameter function 140ff
Moli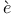 re, G. 46 236 re, G. 46 236
Morse, P. M. 1 20 202 236 237
Newton, R. G. 35(28) 36(28) 179(28) 217(28) 234(51) 236 237
Nicholson, J. W. 238
Number of bound states 150 153 187 228 239
Numerical computation of bound state energies 173
Numerical computation of pole functions 160
Numerical computation of scattering phase shifts 20 21ff 112
Olsson, P. O. 2(6) 236
Partial wave amplitude 5
Parzen, G. 125 236
Percival, C. 239
Perlmutter, A. 2(22) 140 141(22) 236
Phase equation 11ff 13ff 87ff 116ff 124 127ff 130ff
Phase functions 11ff 13ff 18 21ff 115ff 130
Phase functions, radial wave function and 31ff 86ff 130
Phase shift see “Scattering phase shift”
Pole equation 145ff 154ff 225ff
Pole function 145ff 154ff 223ff
Potential, centrifugal 4 81 89ff 108 151
Potential, complex 132ff
Potential, Coulomb 3 78ff 128 154 235
Potential, Dirac distribution 53 185 194
Potential, effective for Dirac particles 122
Potential, exponential 189
Potential, Hulth n 190 n 190
Potential, infinitely repulsive 15 103 108
Potential, inverse power 110
Potential, multichannel 136ff
Potential, nonlocal 129ff
Potential, piecewise constant 160ff
Potential, regular 4
Potential, separable 132
Potential, singular 4 97ff
Potential, square-well 18 65 82ff 154ff 185 187 189 194
Potential, Yukawa 21ff 59ff 89 160 194
Radial wave function see “Wave function radial”
Ravenhall, D. G. 2(17) 113(17) 115(17) 116(17) 119(17) 120(17) 236
Reactance matrix 137 139ff
Regge, T. 234(52) 237
Rimini, A. 239
Roberts, M. J. 239
Rosendorff, S. 46 236
S matrix 77 133 137
S matrix function 72 35 133 138ff 221
Scattering amplitude 3ff 121
Scattering amplitude function 72 221
Scattering length 69ff 77ff 109ff
Scattering phase shift 5 11 121 124 127 131
Schey, H. M. 239
Schroedinger Equation, radial 4 117 129 136
Schroedinger equation, three dimensional 3 129
Schwartz, J. L. 239
Schwinger, J. 196 197 237
Spruch, L. 2(12) 236 239
Surynarayan, E. R. 238
Swanson, D. R. 2(8) 236
Tangent function 77 17 115
Tani, S. 46 236
Teixeira, A. F. F. 154(36) 235(36) 236
Tiesz, T. 238
UNITS 2 120 136
Variational principle for first-order differential equations 205ff
Variational principle for scattering length 72ff 77
Variational principle for scattering phase shift 48 57
Verde, M. 239
Virtual state 156 233ff
Watson, G. N. 201(45) 237
Wave function, radial 4ff 31ff
Wave function, three dimensional 3 120 129
Wigner, E. P. 41 106 236
Wigner’s theorem 47 106
Wing, G. M. 238
Zemach, C. 2(21) 236
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 gge, S.
gge, S.  gu
gu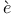 s, J. Y.
s, J. Y.  , N.
, N.