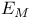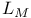|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Krasnosel'skii M.A., Rtuickii Yz.B. — Convex Functions and Orlicz Spaces |
|
|
 |
| Предметный указатель |
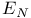 -weakly continuous linear functionals 133 -weakly continuous linear functionals 133
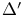 -condition 29 219 -condition 29 219
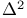 -condition 40 220 -condition 40 220
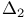 —condition 23 218 —condition 23 218
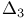 -condition 35 220 -condition 35 220
Absolute continuity of the norm 87
Ahiezer 136 146 239
Albrycht 238 239
Amemiya 231 234 239
Banach 127 134 135 234 239
Banach’s theorem 134
Basis 101
Birnbaum 230 231 239
Branch 208
Branch, point 209 216
Calculation of the norm 88
Carath 6
Carath, conditions 167
Carath, odory 239
Characteristic values 208
Characteristic values, vectors 208
Class of completely continuous operators of continuous operators 137
Compact operator 194
Compactness criteria 94
Comparison of N-functions 14 218
Comparison of Orlicz classes 63
Comparison of spaces 110
Complementary N-function 11
Complete continuity of linear integral operators 149
Completely continuous operator 194
Completeness of Orlicz spaces 70
Composition of N-functions 10
Cone 213
Convex functions 1 217
Differentiability 176 181
Differentiable operator 179
Dinculeanu 232 238 239
Dubrovskii 237 240
Equivalence criterion 17
Equivalent N-functions 15
Fatou’s theorem 71
Fihtengol’c 189 240
Frechet derivative 179
Frechet derivative, differential 179
Frechet’s theorem 97
Gateaux gradient 186
Gateaux gradient, differentiable 186
Glazman 136 146 239
Golomb 236 237 240
Gradient of a functional 176
Gradient of the Luxemburg norm 187 225
Gradient of the norm 176
Gradient of the Orlicz norm 189
Gribanov 232 238 240
Haar 240
Haar, functions 103
Hammerstein 236 237 240
Hammerstein, operator 207
Hardy 230 240
Hille 128 236 240
Holder’s Inequality 72 223
Homogeneous function space 232
Inequality, Hoelder’s 72
Inequality, Jensen’s 1
Inequality, Young’s 13
Integral representation of a convex function 3
Jensen 230 240
Jensen’s Inequality 1
Kalugina 231 236 241
Kantorovic 231 235 236 237 241
Kipriyanov 231 241
Kolmogorov 241
Kolmogorov’s compactness criterion 97 225
Kondrasov 235
Korenblyum 231 241
Krasnosel’skii 167 170 202 212 213 215 230 231 232 233 234 235 236 237 238 241 242
Krein 235 236 237 242 243
Ladyzenski 167 236 237 242 243
Leray 237 243
Levi’s theorem 69
Linear functionals 124
Littlewood 230 240
Lozinski 230 231 243
Luxemburg 78 232 234 243
Luxemburg, gradient of 187
Luxemburg, norm 78 222
Luzin’s C-property 177
Lyusternik 131 236 243
Mean convergence 75
| Medvedev 231 243
Milnes 238 243
Monotonic operator 213
Naimark 244
Nakano 231 232 244
Natanson 6 69 71 94 95 244
Nemyckii 212 236 237 243
Nonlinear integral equations 194
Nonlinear integral equations, operators 167
Norm, Luxemburg 78
Norm, Luxemburg of a functional 134
Norm, Luxemburg of the characteristic function 72
Operator, compact 194
Operator, completely continuous 194
Operator, Hammerstein 207
Operator, potential 214
Operator, Uryson 194
Operators in Orlicz spaces 137
Operators, completely continuous 137
Operators, continuous 137
Operators, differentiable 179
Operators, nonlinear 167
Orlicz 230 231 232 234 239 244
Orlicz, classes 60
Orlicz, gradient of 189
Orlicz, norm 67 221
Orlicz, operators in 137
Orlicz, space 69 221
Partially ordered set 15
Phillips 240
Pinsker 237 241s
Positive operator 213
Potential operator 214
Povolockii 236 242
Principal part of an N-function 16
Product of functions in Orlicz spaces 117
Properties of N-functions 7
Radon 234 244
Riesz 234 244
Riesz’s criterion for compactness 99 225
Rohlin 234 244
Rutickii 230 231 232 234 235 236 237 238 242 244
Rutman 237 243
Salehov 126 234 245
Schaffer 245
Schauder 237 243
Schauder’s principle 209
Scorza Dragoni 212 237 245
Separability of 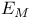 81 81
Set of complete measure 17
Silov 245
Silov’s theorem 233
Simko 232
Skvorcov 245
Sobolev 131 232 233 235 236 242 243 245
Solomyak 233 245
Space 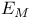 80 80
Space 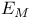 , , 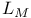 67 67
Space 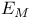 , Orlicz 69 , Orlicz 69
Spectrum 208
Splitting of a completely continuous operator 164
Splitting of a continuous operator 146
Sragin 238 246
Steklov functions 95
Sudakov 233
Sz. — Nagy 234 244
Szegoe 230 244
Takahashi 246
Tamarkin 233 246
Theorem on branch points 216
Theorem, Fatou’s 71
Theorem, Frechet’s 97
Theorem, Levi’s 69
Theorem, Silov’s 233
Theorem, Vallee Poussin’s 94
Theorem, Zaanen’s 155
Tulaikov 233 246
Uryson 246
Uryson, operator 194
Vainberg 186 236 237 246
Vallee Poussin’s theorem 94
Videnskii 238 246
Vulih 237 241
Weiss 238 246
Yamamuro 231 232 247
Young 247
Young’s inequality 13
Zaanen 235 243 247
Zaanen’s theorem 155
Zygmund 230 231 232 247
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



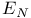 -weakly continuous linear functionals
-weakly continuous linear functionals 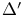 -condition
-condition 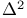 -condition
-condition 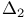 —condition
—condition 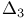 -condition
-condition